Ladder testing and why it most likely won’t be a good use of your time and ammunition
This is a follow up to my post in @Bagheera ’s thread on the reasons forum members might decide to re-run a ladder test. I got a bit sidetracked as to why I didn’t think there was a good reason for shooting ladders in the first place, let alone repeating the process. So when in that thread @Rossi45 asked the question:
I thought I’d pull what was intended as a follow-up into a separate thread and base my explanation around some model examples.
Let’s start out then with a perfect rifle firing perfect ammunition and use this to shoot an imaginary ladder. The rifle is perfect because it will put ammunition that is all exactly the same into the same hole every time, no spread whatsoever. The ammunition is also perfect because having decided on the range of charge weights to be used to shoot the ladder, these are able to be weighed out exactly and no other parameters of the ammo vary between each of the loads.
The ladder is going to be shot in 0.2 grain steps, nine shots in all. There is no need to build this example around shooting groups at each charge weight. With perfect equipment single shots are equally as good since there are no dispersion factors to allow for. I’ve come up with the pattern below that can be used to demonstrate interesting aspects of ladder testing. The grid shown is ½ MoA. Let’s say the target is at 200 yards. That makes the bullet holes below about 6.5mm across. The powder weights themselves have been added mainly as labels. Maybe the fictitious rifle is chambered in 260AI or similar.
Completely hypothetical and unrealistic but with the perfect-rifle-and-perfect- ammunition combination any load provides the same precision as any other – that is multiple shots at a fixed powder weight always form a single hole at the positions shown.
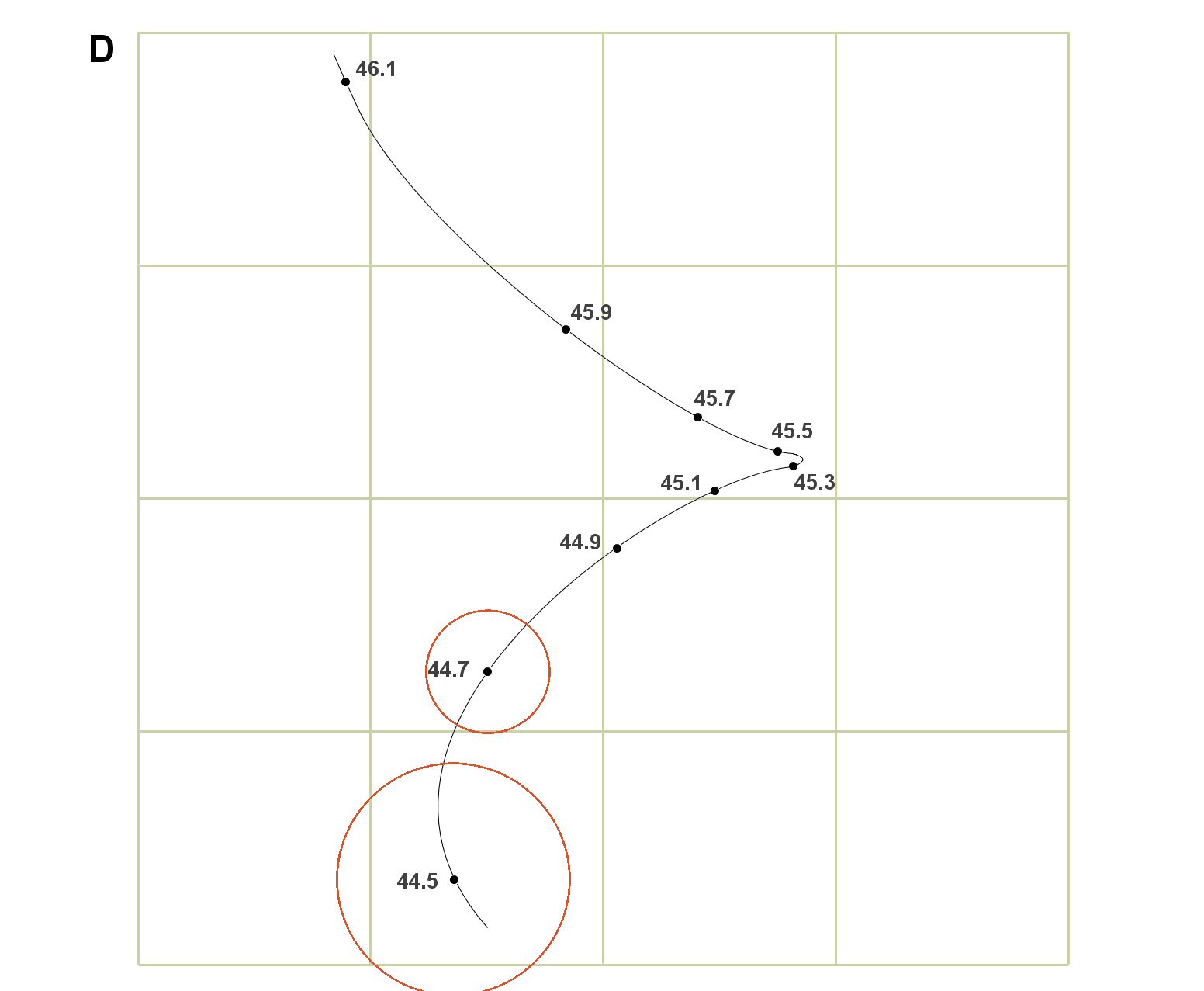
The impact centres can now be plotted and a path of best fit applied by interpolation.
With reference to the charge weight labels, between 44.5gr and 44.7gr at the bottom of the drawing there appears to be a horizontal null, but there isn’t in the vertical direction – in fact the points of impact are tracking upwards quite rapidly with increasing powder charge.
However between 45.3gr and 45.5gr the barrel appears to have reached the far end of its travel in a horizontal sense and is undergoing a reversal, while at the same time the rate of vertical point-of-impact rise with increasing powder has slowed right down. Few would disagree that a 45.4 grain load looks to be at the centre of a very nice ladder node.
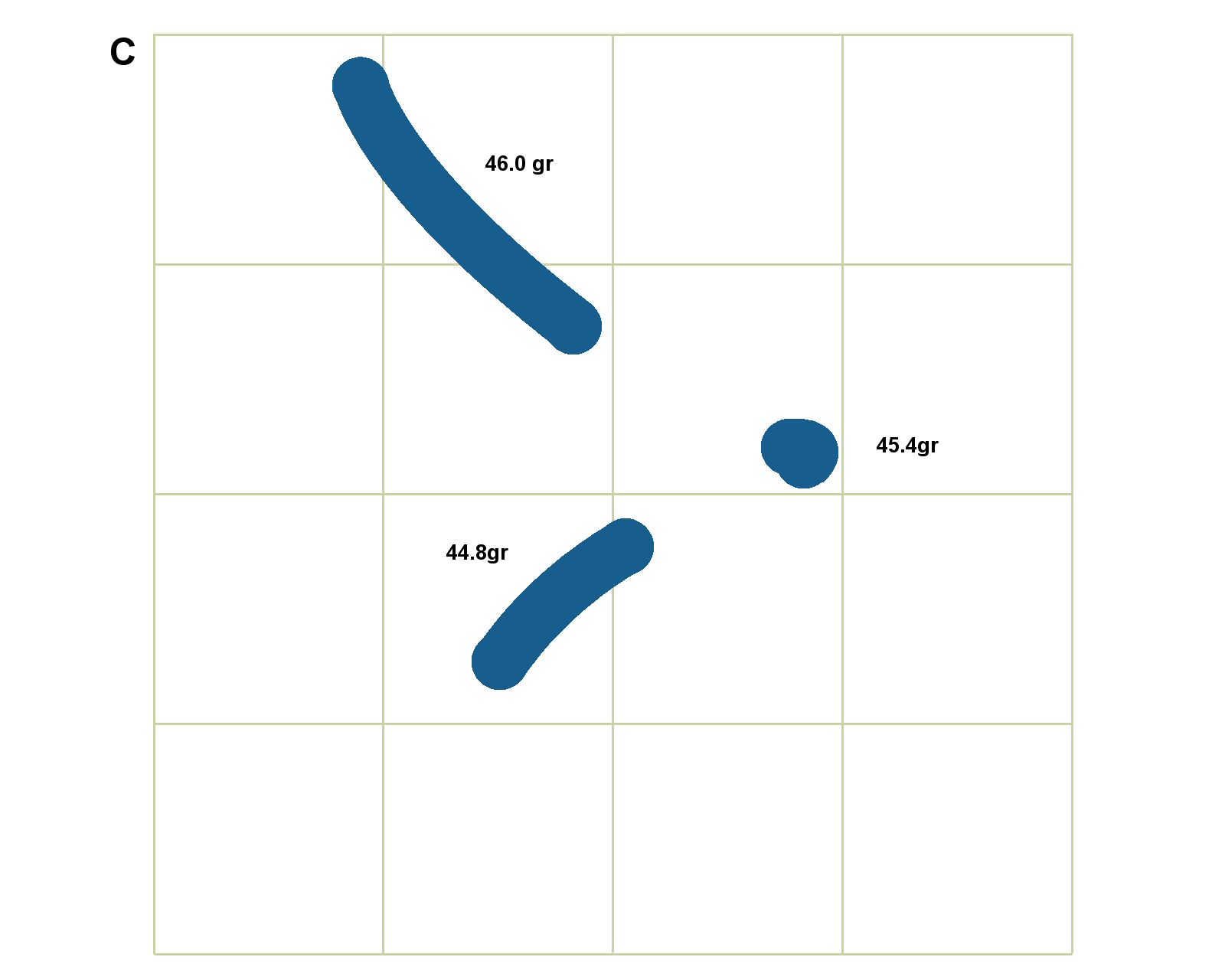
Now we have this information another “shoot” is carried out with many shots at each of three different powder charges within this range to see what benefits operating at a ladder node confers.
The three loads chosen are 44.8gr, 45.4gr, and 46.0gr. The imaginary perfect rifle will still be assumed, but the quality of the ammunition will be relaxed back towards real life. The introduced variation in the ammunition is equivalent to ± 0.1 grains of powder around the nominal powder charge figures. You may disagree but I think this still describes excellent ammunition. If all reloading and ballistic variables in the ammo could be combined and equated to a ± 0.1gr powder variation then .260 shooters would tell us we would typically be expecting muzzle velocity ES close to 14ft/sec. Here is the target we would expect to see:
It can be seen that this ammunition is still restricted to hitting along segments of the line traced in drawing B. The spread along the line is a result of the newly introduced variability in the powder charges. For example each round of the 46.0gr ammo may contain anywhere between 45.9gr and 46.1gr of powder, so the trace at the top showing where the imaginary shots hit the target must necessarily stretch between these two positions copied over from drawing B. The 0.2gr spread from B has also been copied over for the other two loads centred on 45.4gr and 44.8gr. We are still using the perfect rifle however so there is no other source of variation. The lines of shots are still only one calibre wide. The benefit of loading for the ladder node centred on the charge weight of 45.4grains is obvious.
From my previous post on the reasons for wanting to operate at a ladder node:
“...variation in the ammunition will have a lower impact on the change in position of the shots on average than it might otherwise have if ammunition was loaded to be away from a ladder node.”
Now the perfect rifle can be substituted with a “real” one. This change is intended to allow examples to be built up that support an assertions made in my earlier post in the other thread: that it becomes progressively less likely that useful information can be extracted from a ladder test as the behaviour of the rifle and ammunition declines from the above perfect example.
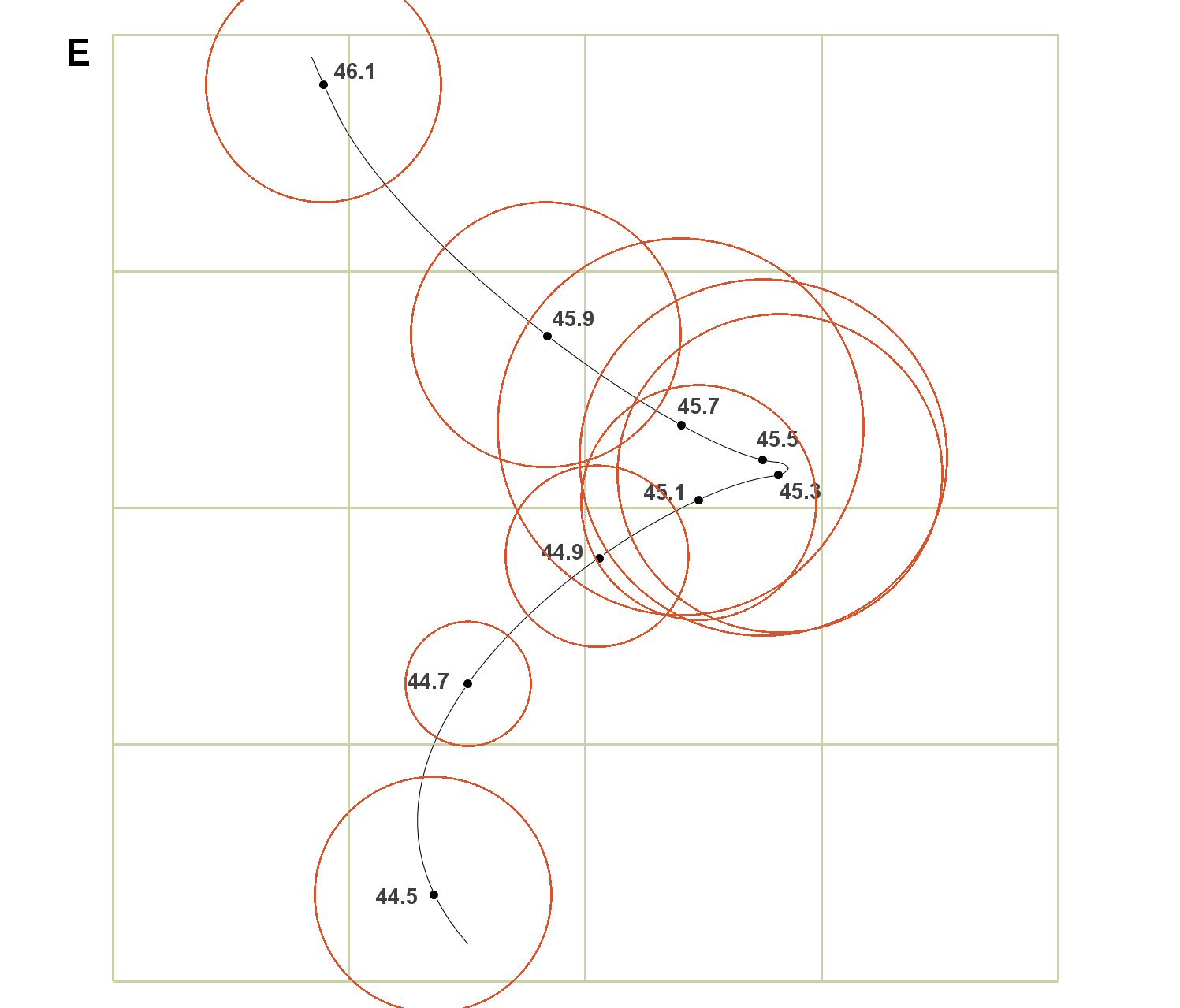
So we move to a simulated rifle modelled on more realistic properties, still a very good one however. With the right load it will put 90% of shots into ¼ MoA at 200 yards with perfect ammunition. Not your average hunting rifle then. I’ll set it up to do this for a powder charge of 44.7gr. At 44.5gr it shoots ½ MoA. I just made these figures up for the purposes of this example. 90% probability boundaries can be drawn around the original points that now represent group centres.
For this rifle it seems fair to have it shooting maybe as poorly as ¾ MoA groups for a load it doesn’t like. I’ll make this at 45.7gr. The other powder charges can deliver groups between the two extremes as shown in diagram E below where all the probability boundaries have been added.
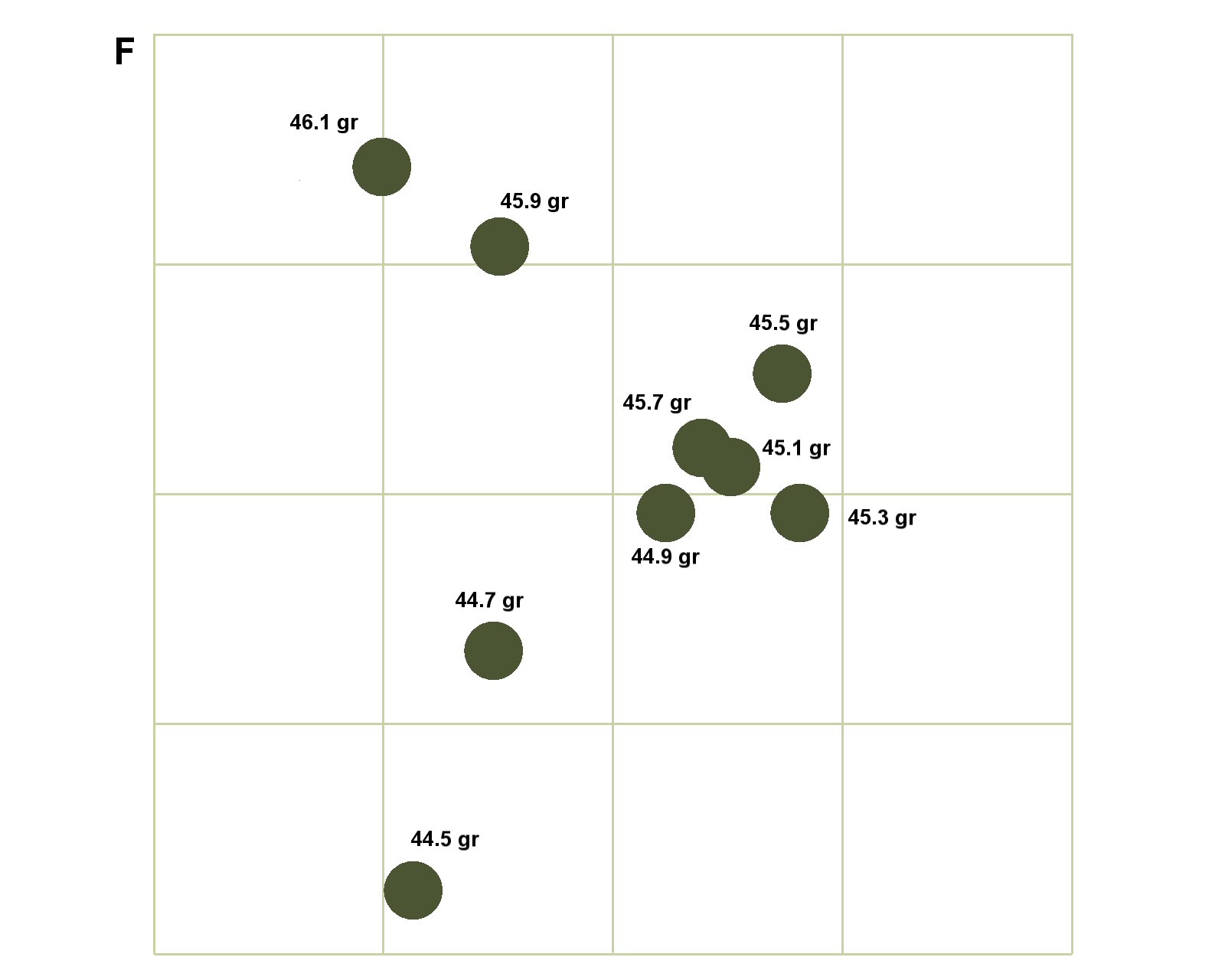
Now the imaginary ladder test is repeated using nine shots again, one for each charge weight as it was for A. Note that the shot loaded with 44.7 grains of powder hits the target very close to where it did from the perfect rifle because (as was decided earlier) accuracy remains very good for this load. For the other charge weights I’ve spread the individual shots around a bit within their allowable limits – still mainly close to the group centres though as the expected distribution profile requires.
The problem that is beginning to appear is that the positions where individual shots hit may no longer be particularly good representations of the true group centres. The shots around the previously identified ladder node in particular are starting to become a bit jumbled. It’s not too bad a situation however since probability is in favour of shots still falling close to the group centres. There is likely to be the odd shot throwing a spanner into the works that could perhaps in combination with its adjacent charge weight be incorrectly interpreted as a node. Actually since we were dealing with 90% probability boundaries then over nine shots there is more than an even chance of one or more shots shot falling completely outside their respective boundaries. Remember too that in the real world we would not have the benefit of the understanding provided originally by the perfect rifle and ammunition - target F above would become our starting point.
ACTUALLY IT WOULDN’T. No, the situation would be worse than this because in all the excitement I forgot that I was still placing the shots in F. using THE PERFECT AMMUNITION.
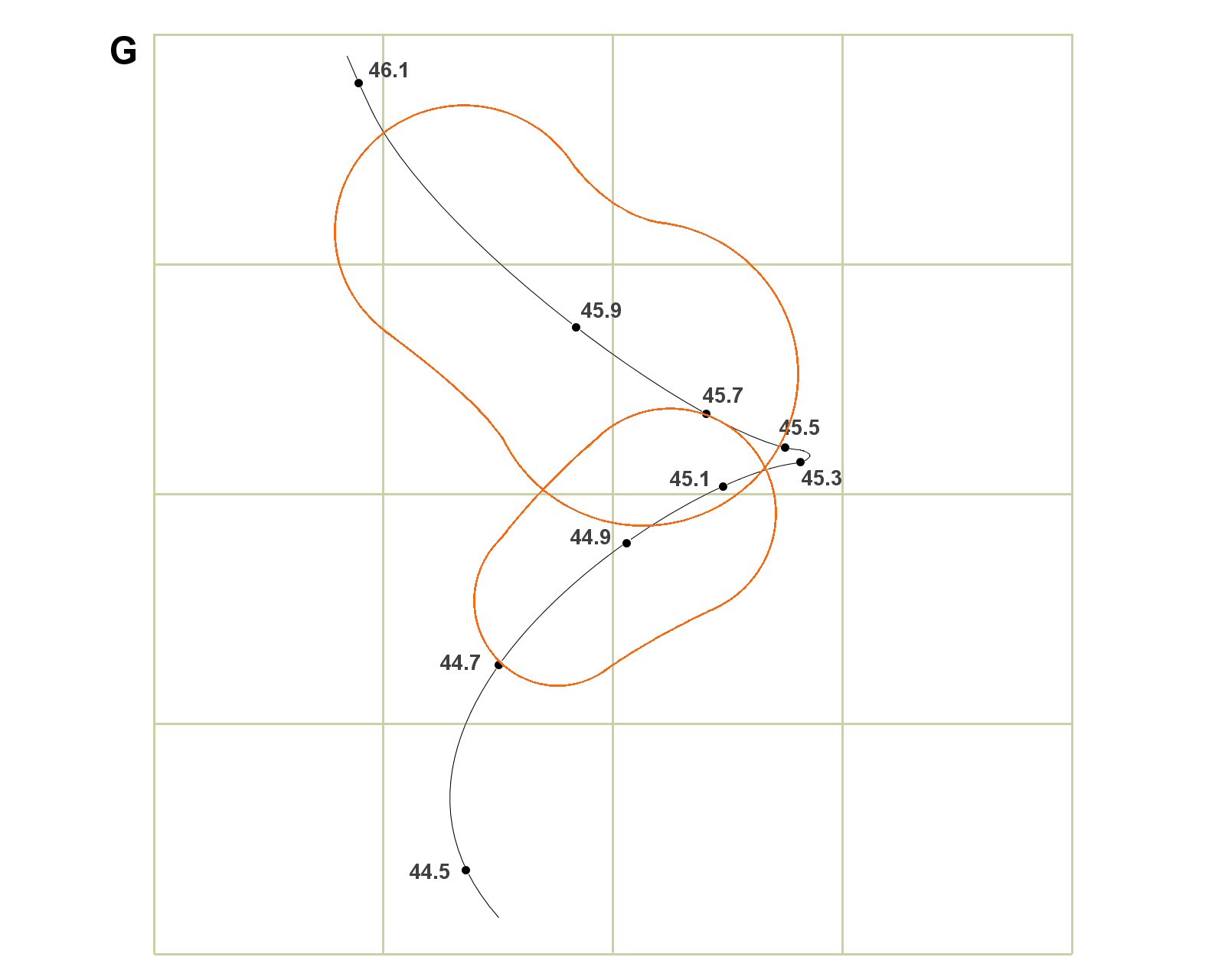
So it is back to the drawing package and diagram E needs to be modified to extend the regions where a shot could likely fall for each nominal powder charge. I’ve started doing this in drawing G - for the “real” rifle AND the “real” ammunition.
I’ve only added two of the extended regions as the drawing would rapidly becoming a mess to interpret at this stage with more. The ammo loaded for 44.9gr - now having the equivalent of a ± 0.1gr tolerance - could range between 44.8gr and 45.0gr. The extremities of the boundaries may look to be wider than this but are in fact centred on these two values. The same has been applied to the other load drawn in and centred at 45.9gr. For the mathematically inclined it will be clear that these probability regions are only indicative for now because to simplify things I’ve given the ammo a uniform distribution between the upper and lower weight limits.
No point really in completing this drawing or posting another drawing of a fictitious ladder of the nine shots as I did in F. What is becoming clear is that in the real world when targets like these form the starting point for a conventional ladder interpretation, the chances of extracting anything meaningful can be... unlikely. This simulation is for a high performing target rifle with match ammo too. Picture the drawing G above with 1 MoA distributions from the rifle for many of the loads and with the ammo also more variable, then visualise the possible fall of the nine shots.
Here was another assertion I made earlier:
Even if a genuine ladder node could for found, for real rifles with real ammo, it is a more effective use of time and ammo to instead find and shoot a load within the velocity range required that provides the smallest group by circular/random distribution. Operating at this type of node will improve the chances of single or multiple shots hitting close to the point of aim far more than at a ladder node – often dramatically so.
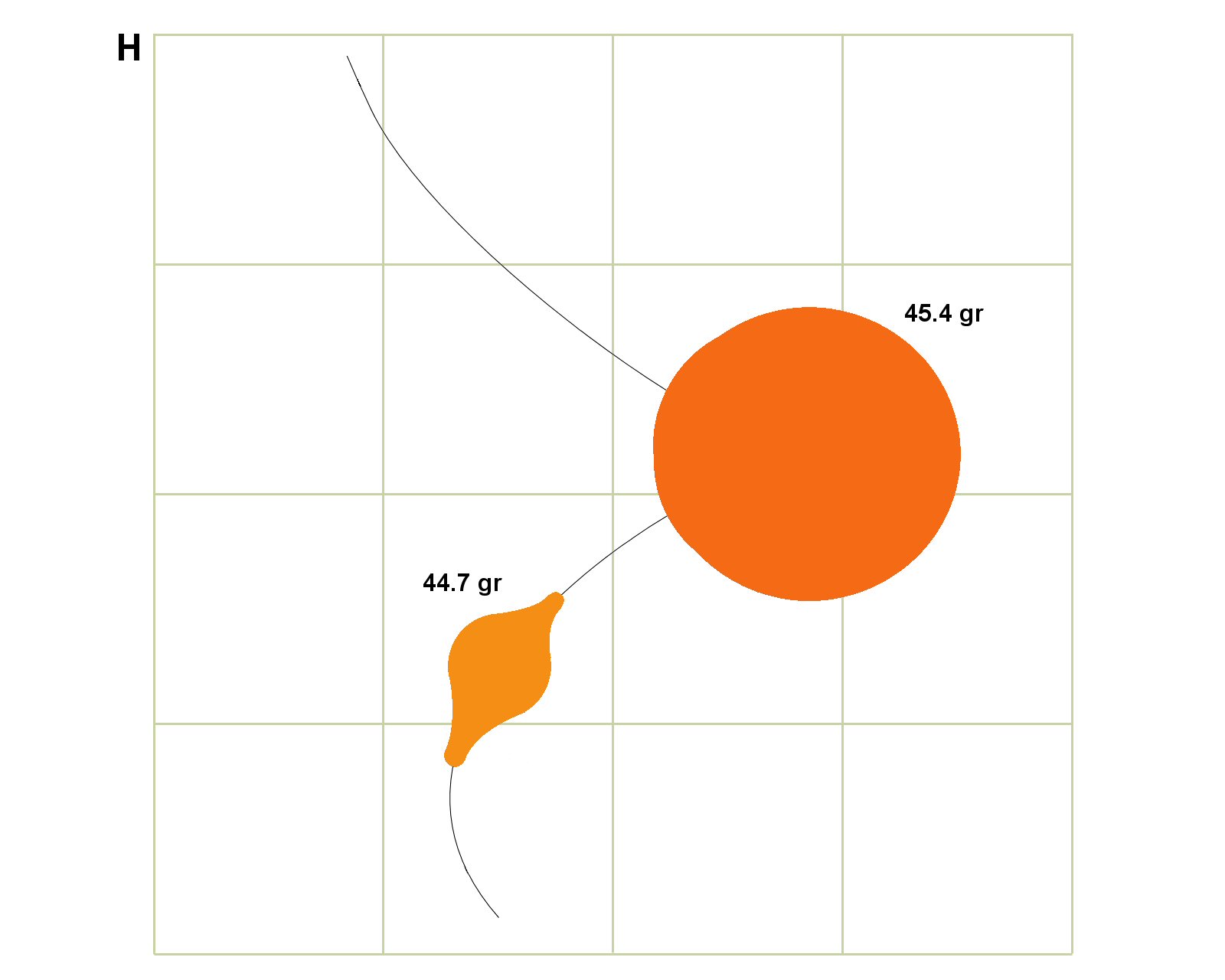
And this too can be demonstrated as follows. Sticking with the same real rifle with real ammo with the same properties: if by good fortune the fall of the shots in the ladder test had allowed us to deduce correctly that a ladder node was at 45.4gr as it has been throughout all these examples, and from some other methods of testing - shooting for groups say - we knew that a load of 44.7gr shot ¼ MoA, again as in the earlier example (see E.), then let’s compare what these two particular loads might look like on a target after many shots are fired for each.
Here we see the 90% probability regions for ammunition loaded for the ladder node (darker orange) and for the powder weight that provides the tightest groups in a circular/random sense (light orange). This is for ammunition loaded with the previously described ± 0.1gr weighing tolerance, and unlike in G I’ve made an effort here to better predict the shape of the combined distributions (rifle and ammo superimposed). Certainly at the ladder node the centre of the group barely moves as before, so the distribution remains close to circular, but is around 0.6 MoA.
Despite the other load being clearly more sensitive to variations in the ammo, it will still provides better results. As the consistency of the ammo is improved, so does the performance margin of the lighter orange load over the darker.
Yes of course I was careful to make sure in my examples that the locations of the two different types of node did not coincide. And I let the rifle shoot 0.6MoA at the ladder node. Have I unfairly hamstrung ladder testing in the examples? I don’t think so. What are the chances of the two types of node actually coinciding? If you are fortunate enough to have a ladder node occurring for the same charge weight as a group size minimum then you are very lucky indeed.
Is a ladder test useful for anything?
As has been posted recently by several on here, if loads are being incrementally increased while looking for the onset of pressure signs why not shoot at a target. Just don’t read something into the pattern of shots that has only been thrown up by chance.
If you simply won’t be deterred from the concept of ladder testing then do I think there are any steps that can be taken to improve the chances of getting meaningful results on the target?
— Only test rifles that tend towards the earlier perfect rifle and shoot small groups with most or all of the test loads. (No, finding loads that shoot small groups is not why we are shooting a ladder in the first place. If you still think this you need to go back to GO and not collect $200.)
— Go with the OCW method and shoot 5-6 shot groups at each charge weight rather than single shots and so average out both the variation in the rifle and the ammunition. You may choose to shoot these groups Round-Robin as a means of also averaging other variation occurring throughout the test shoot.
— Prepare and use the best ammunition you can manufacture.
— Shoot the ladder at longer ranges. Ideally groups will only become proportionally larger at longer ranges (ie a 1MoA group at 100m will remain so at 300 or 400m, whereas drop increases by a little under the square of distance, so the ladder will spread out faster than the areas within which each shot could fall and so be easier to interpret correctly.
— Only ladder test rifles where the barrel moves the impact points around a lot with different charge weights. This also spreads out the shots across the target and improves the chances of the bunching up of shots being the result of a genuine ladder node rather than a chance occurrence.
Welcome guest, is this your first visit? Create Account now to join.
Welcome to the NZ Hunting and Shooting Forums.
Search Forums
User Tag List
+ Reply to Thread
Results 1 to 15 of 16
Thread: Ladder Testing
-
04-11-2018, 04:20 PM #1
Ladder Testing
-
-
04-11-2018, 04:59 PM #2Member

- Join Date
- Jul 2012
- Location
- North Shore Auck
- Posts
- 665
So to distill this down to a more manageable , and readable , synopsis . You have made up a load of crap to justify the fact that Ladder testing is used by fools . If I was to want to prove Ladder testing was Crap , I would actually do real testing to prove it , not have a discussion with my pet pink elephant .
I mean come on use real data not imaginery crap to support your stance , how can someone argue the counter when you control the data ?? .
-
04-11-2018, 05:12 PM #3
My type of ladder test is useful. Test my scope clicks and ammo vs the strelock results. Handy for seeing where mil-surp sight settings end up putting modern ammo as well.
Nothing techo just a board or old box, a marker pen, tape and a level. App says where the bullet will be at 100m if your sights set to 1,2,3,4...whatever hundred setting on the opens you want. shoot the cross at the bottom set on your zero or hundy setting. measure and see if t. Then shoot a group at each sight setting. measure how high up from the base target and see if they match what your app/calculator said they should be.
Best part of this test is you get to shoot heaps of groups.
-
04-11-2018, 06:07 PM #4Member

- Join Date
- Jul 2012
- Location
- North Shore Auck
- Posts
- 665
I use a " Ladder test " to find an accuracy node , cause I'm to cheap and lazy , and then confirm with a group testing . I don't decide what the results are before I decide the outcome .
-
04-11-2018, 06:16 PM #5Member

- Join Date
- Jul 2012
- Location
- Napier, Hawkes Bay
- Posts
- 4,460
Ladder testing is also good for determining max safe powder charge and at what level you see excess pressure signs etc.
-
04-11-2018, 06:17 PM #6
I ladder test all the time now and save so much in components and time developing a load, get better results than the old fashioned "load up 3 at each charge weight" also. Short story, it works.
Flappy Disc Customs Bespoke Hunting Rifles
-
04-11-2018, 07:02 PM #7
My post began with examples based around a hypothetical perfect rifle using perfect ammunition. Simulations are used where the source of data or observations are not available. There is no issue with simulations provided the starting criteria are well defined - then the results can be understood in light of these.
Here are two alternatives for you to consider to address your concerns:
Provide some alternative simulated data that proves that it is possible to find ladder nodes with the sort of rifles and ammunition forum members use, and then go on to show how this will improved the groups they can shoot,
or
supply some real-world data with the same objective.
By all means cling tightly to your concept of ladders. It seems to me you have been shooting for groups and not to find ladder nodes. This was the alternative that I recommended. So we’re all good, right ?
-
04-11-2018, 07:09 PM #8
-
05-11-2018, 08:56 AM #9
thank you @Puffin for taking the time to post this thread, would have taken you a good amount of time . . some food for thougth there
R.without a picture . .. it never happened !
-
05-11-2018, 10:48 AM #10
With the exception of shooters whose passion is target, or benchrest, etc is there any advantage in doing this, or playing with seating depth, neck tension and a whole host of other things if you are achieving accuracy that you are happy with as things stand.
Puffin didnt mention variables like barrel temperature rise, unconscious changes in cheek weld pressure, shifts in front support loading, bullet weight deviations, barometric effects etc etc. All of these either in conjunction or singly would surely result in erroneous results that could hide any real differences. Im guilty as most of us probably are of picking one result out of a test shooting series that fits what I wanted to see, only to find out it was an error due to some other factors changing.
-
05-11-2018, 12:07 PM #11Member

- Join Date
- Mar 2012
- Location
- Christchurch
- Posts
- 1,491
Thanks Puffin - really interesting. Made me think a bit more about 'accuracy'.
-
05-11-2018, 06:38 PM #12Member

- Join Date
- Mar 2012
- Location
- Waikato
- Posts
- 2,175
-
06-11-2018, 11:27 PM #13Member

- Join Date
- Mar 2012
- Location
- Waikato
- Posts
- 2,175
Here is a ladder I did for my 6.5 Grendel last week.
I used 5 widely spaced powder weights and two sorts of primers.
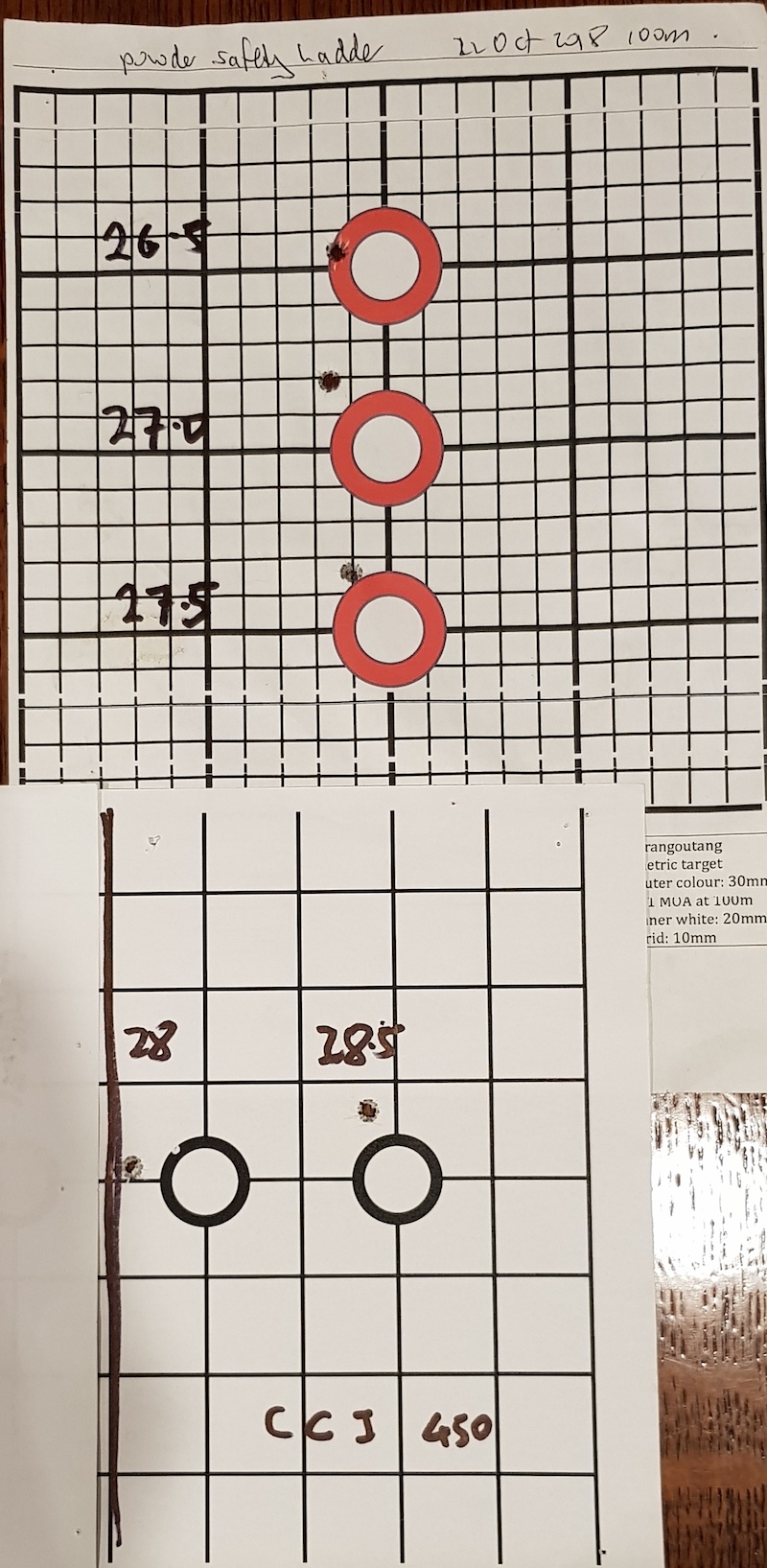
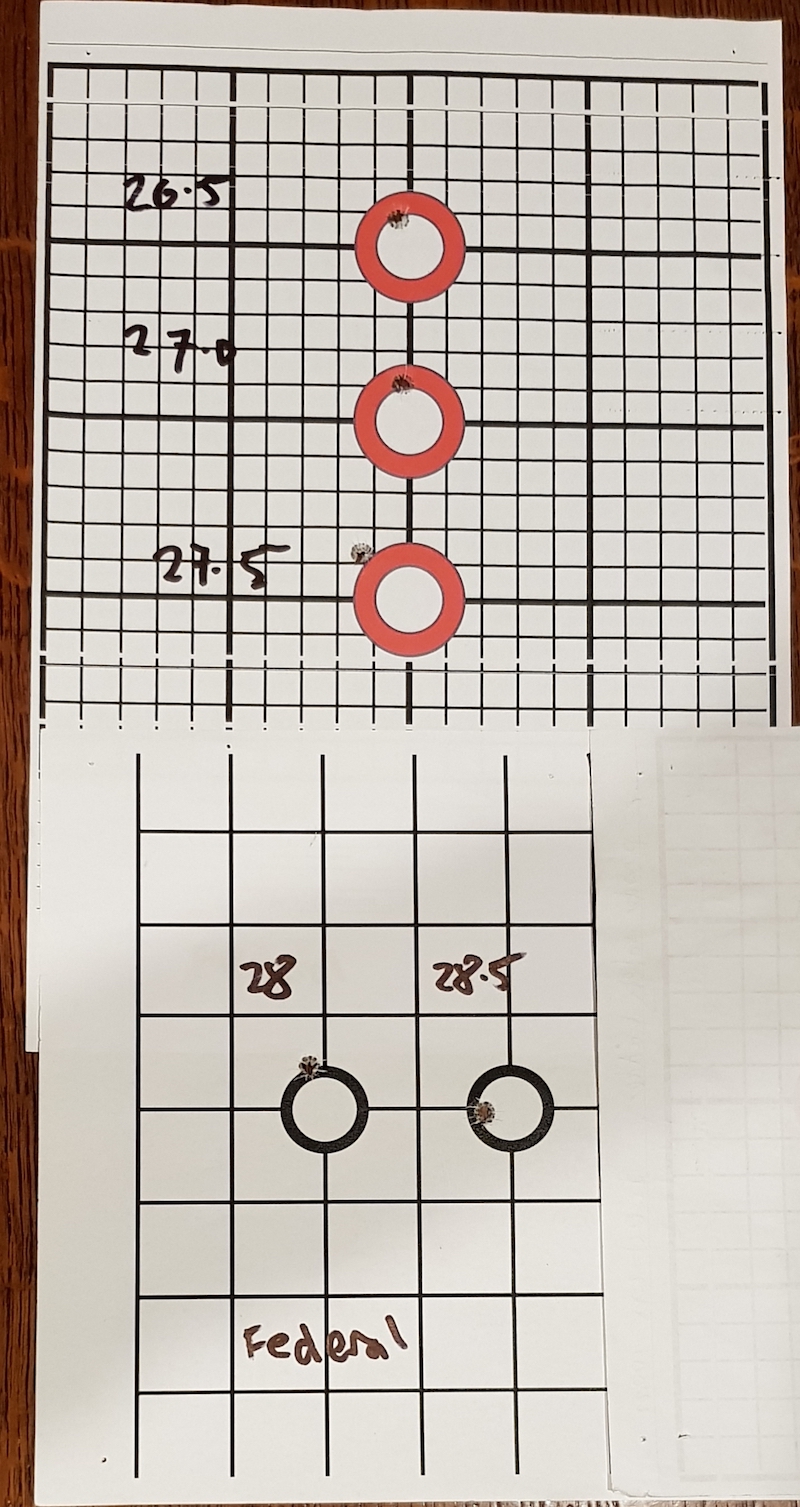
Here are plots of the points of impact of the 5 shots with each primer type:

As you can see there is no real pattern or node. One is simply a 2cm group and the other an apparent 1 cm group. Who would need to measure powder weight when a range of 2 grains will group them pretty much together ?
I chose which powder weight I'd use by:
1. One full grain below the max I'd tested and hadn't ruptured on me.
2. Not a compressed load. I guessed this by measuring the length of the loaded round. I've found in the past that after seating the bullet the compressed loads are a bit longer than they should be. Perhaps the press springs a bit meeting a hard powder charge and can't seat the bullet as deep as it should. My target case base to ogive length was 1.700". The length OAL to tip was a bit more variable. I imagine that 28.5 gr was compressed here and one manual said it would be.
3. And I measured the case base diameters before and after firing, The calipers are only precise to 0.0005" ie half a thou. so expansion only takes values of 1 thou, 1.5 thou and 2 thou. I decided to accept 1.5 thou. Might regret it later if the cases deteriorate. Here are the figures I used:

I loaded up 50 rounds at 27.5gr of BM8208 and fired another 5 shot group off a simple front rest and rear bag at the bench:

The first shot was the bottom left one from a cold but dirty barrel. I won't read anything into it. It's a 23mm group and somewhat higher on the paper than my first fireforming load.
Next, I shot at 600yd (stepping out from 300 of course ) using a backpack rest, prone, holding the foreend:
) using a backpack rest, prone, holding the foreend:
This is the technique and equipment I would use for longer hunting shots. The grid squares are 1 MOA.


Elevation is about 1.5 to 2 MOA and horizontal somewhat more due to my rudimentary wind reading.
So, essentially, I checked a range of powder loads for safety, didn't find a "node" and chose a powder weight a comfortable margin below the highest I'd proofed at.
The grouping at 100m looks adequate, although of course I won't know for sure till I've fired quite a few more groups as I sight in and check zero over the next few months. Grouping at "medium range" , well beyond the working hunting envelope of the Grendel cartridge, using the backpack was also adequate. So, I will just use that first, almost random, load and not bother to experiment to try and improve it.
-
10-11-2018, 11:27 AM #14
I was hoping that Tankd and/or Ryan would have posted some examples of Ladder Testing where ladder nodes were conclusively found, and that knowing this had resulted in optimising a load for better accuracy, but I can understand why they might not have.
Historically the forum has some more real data and here are links for those interested.
https://www.nzhuntingandshooting.co....ndloads-18625/
OCW testing (using 3 shots per load rather than 1). All data presented. Any movement in the group centres appears below the resolution provided by 3-shot groups.
https://www.nzhuntingandshooting.co....260-rem-40854/
Shot at 285m. No ladder node but the rifle spaces the shots in a way that points to dispersion being VERY low. The indications are that this rifle could be a real tack driver with consistent ammo (otherwise it will vertically string). A follow up post from the OP is needed (and more test results) to draw conclusions relevant to the effectiveness of ladder testing.
https://www.nzhuntingandshooting.co....er-test-13143/
A good demonstration of some points from my original post. Bottom of page 2 the shots are numbered.
https://www.nzhuntingandshooting.co....er-test-38845/
Possible cluster. Needs confirmation from the OP that a ladder node was genuine, and whether this then allowed better grouping for this load than any other.
https://www.nzhuntingandshooting.co....t-issue-11027/
Ladder appears promising, but 3-shot groups using the ladder node load are then large. This either shows that single shot (conventional) ladders can show spurious clusters, or that operating at a ladder node load is not a guarantee of tight groups, or both.
https://www.nzhuntingandshooting.co....uestion-35984/
This last link doesn't have any pictures sorry. I've included this only because it contains a completely incorrect description of what ladder testing is. What is described is shooting for best group size while incrimentally increasing powder charge, and to find a safe maximum load. Nothing wrong with this. As I've pointed out - more than once - this is is also my recommendation (not with 3-shots per load however).
-
21-12-2018, 03:58 PM #15Member

- Join Date
- Dec 2018
- Posts
- 9
I have taken a new rifle, broken and fired a ladder on wed evening, tested loads on thursday (less than 50 rds fired total) and loaded friday evening and won Virginia state 1000 yard on Saturday and Sunday.
One part with a ladder that most people miss is recording individual MV for each shot. When you hit a node the MV will go from say 20 fps jumps to around 6-8 and then jump back up after 3 shots to 20 fps again. If you look at your grouping AND your MV groups where they coincide will be your nodes.
Similar Threads
-
First Time Ladder Testing - 260 rem
By nak in forum Reloading and BallisticsReplies: 8Last Post: 16-03-2018, 10:12 AM -
Where to from here (ladder test)
By PerazziSC3 in forum Reloading and BallisticsReplies: 5Last Post: 28-11-2017, 11:58 AM -
223 ladder test
By 25/08IMP in forum Firearms, Optics and AccessoriesReplies: 4Last Post: 17-12-2015, 09:09 PM -
Starting a Ladder for T3 7mm Rem Mag with 162gr A-max's
By Carpe Diem in forum Reloading and BallisticsReplies: 18Last Post: 20-10-2014, 10:00 PM -
Interpreting a Ladder Test
By P38 in forum Reloading and BallisticsReplies: 36Last Post: 17-04-2014, 12:10 AM
Tags for this Thread
Welcome to NZ Hunting and Shooting Forums! We see you're new here, or arn't logged in. Create an account, and Login for full access including our FREE BUY and SELL section Register NOW!!




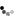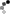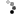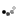
 37Likes
37Likes LinkBack URL
LinkBack URL About LinkBacks
About LinkBacks



 Reply With Quote
Reply With Quote


Bookmarks